はじめに
財務データを取り扱っていると、期中平均の値が欲しいときがあります。
特に、貸借対照表はあくまでもストックデータであり、期首や期末の定点的なデータなので、その途中の平均的な値が欲しいといった場合があると思います。。
例えば、在庫データで考えると、期首と期末で、次のような数字であったとき、どちらの値を採用したらいいでしょうか。
期首:100
期末:1,000
期末の1,000を考えると、期首の100は小さすぎるので、期首の値は採用できず、逆に期首の100を考えると、期末の1,000は大きすぎるので、どちらの値も採用しにくいと思います。
そうしたときに、その途中の期中平均の値を求めたいと思うでしょう。
計算式
期中平均については、計算式は簡単です。
期中平均 = (期首の値 + 期末の値) ÷ 2
平均なので、2つのデータを足して、2で割ればいいというわけです。
単純ですね。
考え方
ただ背景には、次のような考えがあります。
期首はx0、期末はx1の値だったとしましょう。それぞれはあくまでも一時点の瞬間的な値なので、その途中の量を知る必要があります。
これを図で表すと、図の台形の面積を知りたいということになります。
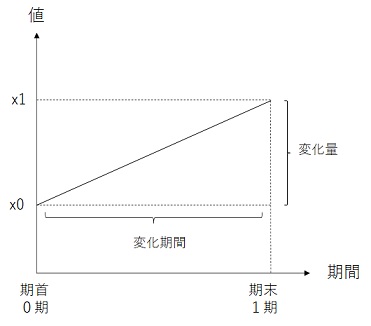
この台形の面積は、次のように計算できます(まさしく台形の公式です)。
台形 = (x0 + x1)×(1期 – 0期)÷2
(1期-0期)は、1期間なの1とすると、
台形 = (x0 + x1)÷2
となり、まさしく期中平均の式になります。
すなわち、期中平均とは、期間中の量を計算していることになります。
また、次のようにも考えられます。
下図を見てください。
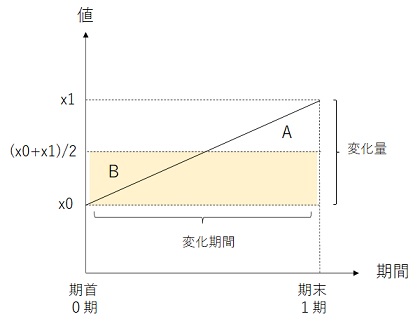
三角形のAとBが同じになるように、補助線を引くとすると、(x0 + x1)÷2で補助線を引くことができます。
そうすると、変化量はうすだいだい色の部分になるので、(x0 + x1)÷2で面積を求めればいいことになります。
ポイント
色々と書きましたが、考え方のポイントとしては、
・(図にあるように)期中平均は、直線状の単純な増減を仮定している
・期中平均は、平均的な「量」を求めている
という点にあります。
計算としては簡単ですが、このような考えがあることに注意してください。

コメント